نظام العدد عند المصري القديم
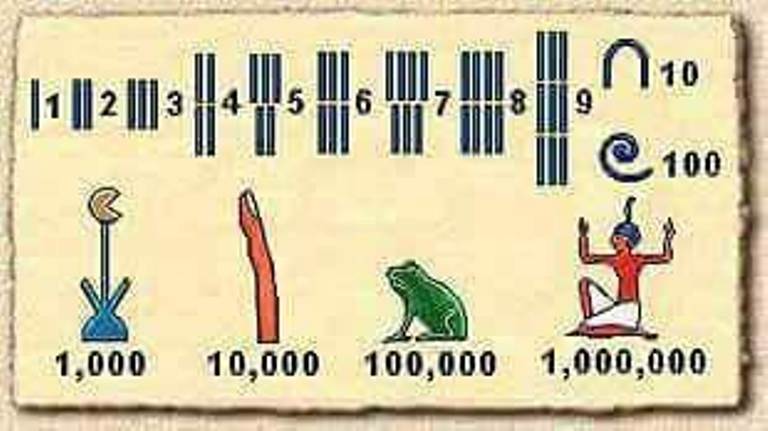
استخدم المصريون القدماء منذ أكثر من 5000 سنة رموزا للأعداد : الواحد ، العشرة ، المائة ، الألف ، العشرة آلاف ، المائة ألف والمليون . ولم يكن لديهم رمز للصفر ، كما أن نظامهم العددي لم بكن يعتمد على فكرة القيمة المكانية (أو الخانة آحاد – عشرات . . . إلخ) بل إن الرمز كان يكرر كثيرا ربما للدلالة على عدد نراه الآن بسيطا – بعد ابتكار النظام العشري ورمز الصفر وفكرة الخانة – وقد كانت اللغة الهيروغليفية هي لغة قدماء المصريين ،
وهي لغة المصريين القدماء . تأخرت معرفتنا بفك رموزها إلى عهد قريب ، حيث عثر (شمبليون) أحد ظباط الحملة الفرنسية على حجر رشيد المكتوب بلغات ثلاث : إحداها الهيروغليفية ، وثانيها اليونانية ، وثالثها القبطية . (انظر الشرح الموسع في أسفل الصفحة) . ومن خلال معرفتنا باللغتين اليونانية والقبطية أمكن فك رموز اللغة الهيروغليفية وقراءة ما سجله المصريون القدماء من نقوش ورسوم على جدران المعابد والهياكل فضلا عن آلاف المخطوطات والبرديات في شتى فروع العلم . وقد أطلق الإغريق (اليونانيون) اسم ” هيروغليفي ” على لغة المصريين القدماء . وهي تعني ” الكتابة المقدسة ” أو ” النقش المصري المقدس ” .
أقدم كتاب في الرياضيات :
إن أقدم كتاب في الرياضيات كتبه على ورق البردى (التفاصيل عن ورق البردى أسفل الصفحة) كاتب اسمه أحمس (ويسمى قرطاس أحمس أو بردية رايند) كُتب منذ أكثر من 35 قرنا – وهو الآن في المتحف البريطاني – وليسس أحمس هو الذي ألف الكتاب بل نسخه من كتاب آخر أُلف في عهد الملك أمنمحـات الثلث حوالى عام 2200 قبل الميلاد أي منذ حوالى 40002 أعوام . كما ظهرت مخطوطات هامة أخرى في الرياضيات مثل بردية موسكو والتي يعود تاريخها إلى قرابة 1850 قبل الميلاد . وتعتبر برديتا ” رايند وموسكو ” هما المصدرين الرئيسيين للمعلومات عن رياضيات قدماء المصريين ، وتتضمن البرديتان (110) مسائل ، وتحتوي بردية رايند وحدها على 85 مسألة ، وهي أول وثيقة رياضية مكتوبة اشتملت على العد وكتابة الأرقام وقواعد العمليات الحسابية الأربع والكسور الاعتيادية والمربع والجذر التربيعي وبعض المتواليات والمسائل الهندسية . كما عرفوا كيف يحلون مسائل نلجأ نحن الآن إلى حلها بالمعادلات الجبرية كمسألة تقول : (كومة كلها وسبعها يساوي تسعة عشر) – وكلمة كومة هذه استخدمها قدماء المصريين للدلالة على أية كمية غير معلومة وتُنطق بصوت يماثل آها (Aha) فإذا صغنا المسألة في لغة العصر لجاءت هكذا (عدد إذا جمع كله على سبعة كان الناتج تسعة عشر) . ومن مبادىء الجبر نعرف أن هذه المسألة يمكن حلها بالمعادلة :
س + س/7 = 19 إذن 8/7 س = 19 إذن س = 133/8 أي أن س = 5/8 16 ولا تأخذ هذه الطريقة في الحل سوى عشر الوقت الذي تأخذه في قراءة الحل كما جاء في قرطاس أحمس – حيث كان يكتب الحل كقطعة طويلة من الجدل الفلسفي . ومن أراد أن يعرف كيف حُلت هذه المسألة في كراس أحمس (بردية رايند) فليرجع إلى كتاب (مقدمة في تاريخ الرياضيات) تأليف الأستاذين د/وليم تاوضروس عبيد ، د/عبد العظيم أحمد أنيس حيث ذكرا في صفحة كاملة ملخصا للحل كما جاء في الأصل .
ومن المسائل التي وردت أيضا في بردية أحمس مسألة تقول : (عدد إذا أضيف إليه ثلثاه ثم أخذ ثلث الناتج يتبقى عشرة فما هو العدد ؟) (من كتاب – أصول تدريس الرياضيات – أ . د . نظلة حسن أحمد . وباستخدام التعبير الرمزي الحديث فإنه يمكن كتابة المسألة هكذا :
س + 2/3 س – 1/3 (س + 2/3 س) = 10 ومنها يمكن إيجاد قيمة س حيث س = 9 وهو العدد المطلوب . أما طريقة المصريين القدماء في حل هذه المسألة فهي أن تأخذ (1/10) العشرة يتبقى 9 ، ثلثا 9 هي 6 بجمعه عليها يكون 15 وثلثه 5 وهي التي أخذت فيكون العدد هو 9 .






